RESISTÊNCIA DOS MATERIAIS
Determine o torque máximo e que pode ser aplicado, em KN.m e o ângulo de torção (rad), sobre o eixo de seção transversal indicada na figura, sabendo que a tensão admissível é de 65 MPa.
Dados: comprimento da barra L = 1,40 m e G = 80 GPa.
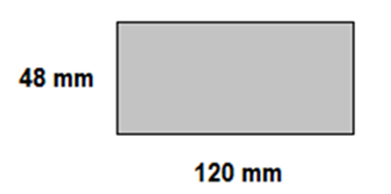
4,64 KN.m e 0,025 rad
3,61 KN.m e 0,015 rad
4,29 KN.m e 0,043 rad
7,42 KN.m e 0,020 rad
4,82 KN.m e 0,050 rad
Determine o estado de tensão equivalente se um elemento estiver orientado a 30o em sentido horário em relação ao elemento mostrado.
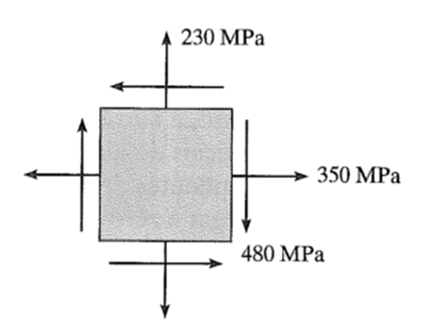
t x' y' = -483.73 MPa
t x' y' = -156 MPa
t x' y' = -188 MPa
t x' y' = -736 MPa
t x' y' = -230 MPa
Determinar aproximadamente o deslocamento (deflexão) máximo que corre na viga a seguir.
y = 22.978/EI
y = 552.8/EI
y = 276.4/EI
y = 677.44/EI
y = 6910/EI
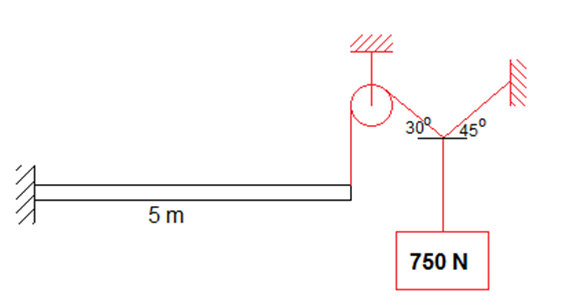
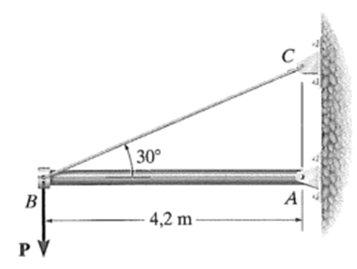
A viga rígida é sustentada por um pino em A e pelos cabos BD e CE. Se a deformação admissível máxima em cada cabo for εmáx = 0,002 mm/mm, determine o deslocamento vertical máximo da carga P.
d = 13,2 mm
d = 15,2 mm
d = 11,2 mm
d = 10,2 mm
d = 12,1 mm
Os dois segmentos de haste circular, um de alumínio e o outro de cobre, estão presos às paredes rígidas de tal modo que há uma folga de 0,2 mm entre eles quando T1 = 15°C. Qual é a maior temperatura T2 exigida para apenas fechar a folga? Cada haste tem diâmetro de 30 mm, αal = 24(10-6)/°C, Eal = 70 GPa, αcobre = 17(10-6)/°C, Ecobre = 126 GPa.
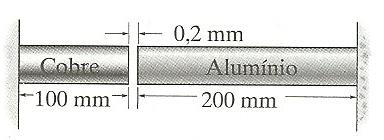
T2 = 43,37 °C
T2 = 45,77 °C
T2 = 42,17 °C
T2 = 46,97 °C
T2 = 48,57 °C
A barra é suportada pelo pino. Se a tensão de tração admissível para a barra for (σt)adm = 150 MPa e a tensão de cisalhamento admissível para o pino for
adm = 85 MPa, determine o diâmetro do pino para o qual a carga P será máxima. Considere que o orifício na barra tem o mesmo diâmetro d do pino. Considere também t = 6 mm e w = 50 mm.
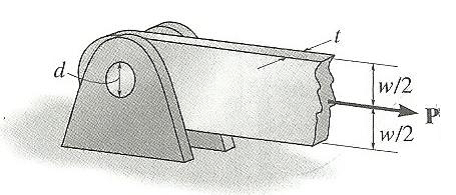
d = 16,29 mm
d = 19,29 mm
d = 18,29 mm
d = 17,29 mm
d = 15,29 mm
O tubo de aço A-36 tem diâmetro externo de 100 mm. Se for mantido no lugar por um cabo de ancoragem, determine, com aproximação de múltiplos de 5 mm, o diâmetro interno exigido para que ele possa suportar uma carga vertical máxima de P=20 kN sem provocar flambagem no tubo. Considere que as extremidades do tubo estão acopladas por pinos. E = 200 GPa.
dint = 95 mm
dint = 60 mm
dint = 80 mm
dint = 90 mm
dint = 45 mm
Uma coluna de aço A-36 (E= 200 GPa) tem comprimento de 4m e está presa por pinos em ambas as extremidades. Se a área da seção transversal tiver dimensões mostradas na figura, determine a carga crítica.
Pcr = 25,7 KN
Pcr = 32,7 KN
Pcr = 22,7 KN
Pcr = 27,7 KN
Pcr = 34,7 KN
A viga é construída com cinco tábuas parafusadas como mostra a figura. Determine a força de cisalhamento máxima desenvolvida em cada parafuso se o espaço entre eles for s = 250 mm e o cisalhamento aplicado for V = 35 kN.
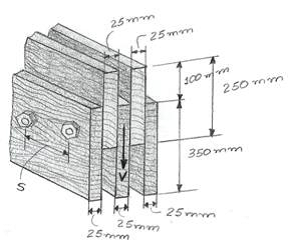
F = 3,31 KN
F = 4,51 KN
F = 8,31 KN
F = 5,31 KN
F = 3,51 KN
Um amortecedor de vibrações é constituído por dois blocos de borracha colados à placa AB e dois suportes fixos, como mostra a figura. Determine o módulo de elasticidade transversal da borracha a ser usada, sabendo-se que, para uma força vertical P de 40 KN, o deslocamento vertical de placa AB deve ser no máximo, 3,5 mm. Considere a = 35 mm, h = 200 mm e espessura = 120 mm e E = 120 GPa.
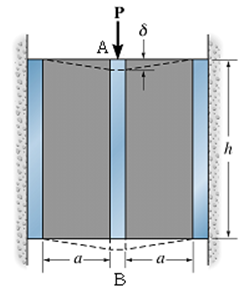
Dados: comprimento da barra L = 1,40 m e G = 80 GPa.
4,64 KN.m e 0,025 rad
3,61 KN.m e 0,015 rad
4,29 KN.m e 0,043 rad
7,42 KN.m e 0,020 rad
4,82 KN.m e 0,050 rad
Determine o estado de tensão equivalente se um elemento estiver orientado a 30o em sentido horário em relação ao elemento mostrado.
t x' y' = -483.73 MPa
t x' y' = -156 MPa
t x' y' = -188 MPa
t x' y' = -736 MPa
t x' y' = -230 MPa
Determinar aproximadamente o deslocamento (deflexão) máximo que corre na viga a seguir.
y = 22.978/EI
y = 552.8/EI
y = 276.4/EI
y = 677.44/EI
y = 6910/EI
A viga rígida é sustentada por um pino em A e pelos cabos BD e CE. Se a deformação admissível máxima em cada cabo for εmáx = 0,002 mm/mm, determine o deslocamento vertical máximo da carga P.
d = 13,2 mm
d = 15,2 mm
d = 11,2 mm
d = 10,2 mm
d = 12,1 mm
Os dois segmentos de haste circular, um de alumínio e o outro de cobre, estão presos às paredes rígidas de tal modo que há uma folga de 0,2 mm entre eles quando T1 = 15°C. Qual é a maior temperatura T2 exigida para apenas fechar a folga? Cada haste tem diâmetro de 30 mm, αal = 24(10-6)/°C, Eal = 70 GPa, αcobre = 17(10-6)/°C, Ecobre = 126 GPa.
T2 = 43,37 °C
T2 = 45,77 °C
T2 = 42,17 °C
T2 = 46,97 °C
T2 = 48,57 °C
A barra é suportada pelo pino. Se a tensão de tração admissível para a barra for (σt)adm = 150 MPa e a tensão de cisalhamento admissível para o pino for
adm = 85 MPa, determine o diâmetro do pino para o qual a carga P será máxima. Considere que o orifício na barra tem o mesmo diâmetro d do pino. Considere também t = 6 mm e w = 50 mm.
d = 16,29 mm
d = 19,29 mm
d = 18,29 mm
d = 17,29 mm
d = 15,29 mm
O tubo de aço A-36 tem diâmetro externo de 100 mm. Se for mantido no lugar por um cabo de ancoragem, determine, com aproximação de múltiplos de 5 mm, o diâmetro interno exigido para que ele possa suportar uma carga vertical máxima de P=20 kN sem provocar flambagem no tubo. Considere que as extremidades do tubo estão acopladas por pinos. E = 200 GPa.
dint = 95 mm
dint = 60 mm
dint = 80 mm
dint = 90 mm
dint = 45 mm
Uma coluna de aço A-36 (E= 200 GPa) tem comprimento de 4m e está presa por pinos em ambas as extremidades. Se a área da seção transversal tiver dimensões mostradas na figura, determine a carga crítica.
Pcr = 25,7 KN
Pcr = 32,7 KN
Pcr = 22,7 KN
Pcr = 27,7 KN
Pcr = 34,7 KN
A viga é construída com cinco tábuas parafusadas como mostra a figura. Determine a força de cisalhamento máxima desenvolvida em cada parafuso se o espaço entre eles for s = 250 mm e o cisalhamento aplicado for V = 35 kN.
F = 3,31 KN
F = 4,51 KN
F = 8,31 KN
F = 5,31 KN
F = 3,51 KN
Um amortecedor de vibrações é constituído por dois blocos de borracha colados à placa AB e dois suportes fixos, como mostra a figura. Determine o módulo de elasticidade transversal da borracha a ser usada, sabendo-se que, para uma força vertical P de 40 KN, o deslocamento vertical de placa AB deve ser no máximo, 3,5 mm. Considere a = 35 mm, h = 200 mm e espessura = 120 mm e E = 120 GPa.
t x' y' = -483.73 MPa
t x' y' = -156 MPa
t x' y' = -188 MPa
t x' y' = -736 MPa
t x' y' = -230 MPa
Determinar aproximadamente o deslocamento (deflexão) máximo que corre na viga a seguir.
y = 22.978/EI
y = 552.8/EI
y = 276.4/EI
y = 677.44/EI
y = 6910/EI
A viga rígida é sustentada por um pino em A e pelos cabos BD e CE. Se a deformação admissível máxima em cada cabo for εmáx = 0,002 mm/mm, determine o deslocamento vertical máximo da carga P.
d = 13,2 mm
d = 15,2 mm
d = 11,2 mm
d = 10,2 mm
d = 12,1 mm
Os dois segmentos de haste circular, um de alumínio e o outro de cobre, estão presos às paredes rígidas de tal modo que há uma folga de 0,2 mm entre eles quando T1 = 15°C. Qual é a maior temperatura T2 exigida para apenas fechar a folga? Cada haste tem diâmetro de 30 mm, αal = 24(10-6)/°C, Eal = 70 GPa, αcobre = 17(10-6)/°C, Ecobre = 126 GPa.
T2 = 43,37 °C
T2 = 45,77 °C
T2 = 42,17 °C
T2 = 46,97 °C
T2 = 48,57 °C
A barra é suportada pelo pino. Se a tensão de tração admissível para a barra for (σt)adm = 150 MPa e a tensão de cisalhamento admissível para o pino for
adm = 85 MPa, determine o diâmetro do pino para o qual a carga P será máxima. Considere que o orifício na barra tem o mesmo diâmetro d do pino. Considere também t = 6 mm e w = 50 mm.
d = 16,29 mm
d = 19,29 mm
d = 18,29 mm
d = 17,29 mm
d = 15,29 mm
O tubo de aço A-36 tem diâmetro externo de 100 mm. Se for mantido no lugar por um cabo de ancoragem, determine, com aproximação de múltiplos de 5 mm, o diâmetro interno exigido para que ele possa suportar uma carga vertical máxima de P=20 kN sem provocar flambagem no tubo. Considere que as extremidades do tubo estão acopladas por pinos. E = 200 GPa.
dint = 95 mm
dint = 60 mm
dint = 80 mm
dint = 90 mm
dint = 45 mm
Uma coluna de aço A-36 (E= 200 GPa) tem comprimento de 4m e está presa por pinos em ambas as extremidades. Se a área da seção transversal tiver dimensões mostradas na figura, determine a carga crítica.
Pcr = 25,7 KN
Pcr = 32,7 KN
Pcr = 22,7 KN
Pcr = 27,7 KN
Pcr = 34,7 KN
A viga é construída com cinco tábuas parafusadas como mostra a figura. Determine a força de cisalhamento máxima desenvolvida em cada parafuso se o espaço entre eles for s = 250 mm e o cisalhamento aplicado for V = 35 kN.
F = 3,31 KN
F = 4,51 KN
F = 8,31 KN
F = 5,31 KN
F = 3,51 KN
Um amortecedor de vibrações é constituído por dois blocos de borracha colados à placa AB e dois suportes fixos, como mostra a figura. Determine o módulo de elasticidade transversal da borracha a ser usada, sabendo-se que, para uma força vertical P de 40 KN, o deslocamento vertical de placa AB deve ser no máximo, 3,5 mm. Considere a = 35 mm, h = 200 mm e espessura = 120 mm e E = 120 GPa.
y = 22.978/EI
y = 552.8/EI
y = 276.4/EI
y = 677.44/EI
y = 6910/EI
A viga rígida é sustentada por um pino em A e pelos cabos BD e CE. Se a deformação admissível máxima em cada cabo for εmáx = 0,002 mm/mm, determine o deslocamento vertical máximo da carga P.
d = 13,2 mm
d = 15,2 mm
d = 11,2 mm
d = 10,2 mm
d = 12,1 mm
Os dois segmentos de haste circular, um de alumínio e o outro de cobre, estão presos às paredes rígidas de tal modo que há uma folga de 0,2 mm entre eles quando T1 = 15°C. Qual é a maior temperatura T2 exigida para apenas fechar a folga? Cada haste tem diâmetro de 30 mm, αal = 24(10-6)/°C, Eal = 70 GPa, αcobre = 17(10-6)/°C, Ecobre = 126 GPa.
T2 = 43,37 °C
T2 = 45,77 °C
T2 = 42,17 °C
T2 = 46,97 °C
T2 = 48,57 °C
A barra é suportada pelo pino. Se a tensão de tração admissível para a barra for (σt)adm = 150 MPa e a tensão de cisalhamento admissível para o pino for
adm = 85 MPa, determine o diâmetro do pino para o qual a carga P será máxima. Considere que o orifício na barra tem o mesmo diâmetro d do pino. Considere também t = 6 mm e w = 50 mm.
d = 16,29 mm
d = 19,29 mm
d = 18,29 mm
d = 17,29 mm
d = 15,29 mm
O tubo de aço A-36 tem diâmetro externo de 100 mm. Se for mantido no lugar por um cabo de ancoragem, determine, com aproximação de múltiplos de 5 mm, o diâmetro interno exigido para que ele possa suportar uma carga vertical máxima de P=20 kN sem provocar flambagem no tubo. Considere que as extremidades do tubo estão acopladas por pinos. E = 200 GPa.
dint = 95 mm
dint = 60 mm
dint = 80 mm
dint = 90 mm
dint = 45 mm
Uma coluna de aço A-36 (E= 200 GPa) tem comprimento de 4m e está presa por pinos em ambas as extremidades. Se a área da seção transversal tiver dimensões mostradas na figura, determine a carga crítica.
Pcr = 25,7 KN
Pcr = 32,7 KN
Pcr = 22,7 KN
Pcr = 27,7 KN
Pcr = 34,7 KN
A viga é construída com cinco tábuas parafusadas como mostra a figura. Determine a força de cisalhamento máxima desenvolvida em cada parafuso se o espaço entre eles for s = 250 mm e o cisalhamento aplicado for V = 35 kN.
F = 3,31 KN
F = 4,51 KN
F = 8,31 KN
F = 5,31 KN
F = 3,51 KN
Um amortecedor de vibrações é constituído por dois blocos de borracha colados à placa AB e dois suportes fixos, como mostra a figura. Determine o módulo de elasticidade transversal da borracha a ser usada, sabendo-se que, para uma força vertical P de 40 KN, o deslocamento vertical de placa AB deve ser no máximo, 3,5 mm. Considere a = 35 mm, h = 200 mm e espessura = 120 mm e E = 120 GPa.
d = 13,2 mm
d = 15,2 mm
d = 11,2 mm
d = 10,2 mm
d = 12,1 mm
Os dois segmentos de haste circular, um de alumínio e o outro de cobre, estão presos às paredes rígidas de tal modo que há uma folga de 0,2 mm entre eles quando T1 = 15°C. Qual é a maior temperatura T2 exigida para apenas fechar a folga? Cada haste tem diâmetro de 30 mm, αal = 24(10-6)/°C, Eal = 70 GPa, αcobre = 17(10-6)/°C, Ecobre = 126 GPa.
T2 = 43,37 °C
T2 = 45,77 °C
T2 = 42,17 °C
T2 = 46,97 °C
T2 = 48,57 °C
A barra é suportada pelo pino. Se a tensão de tração admissível para a barra for (σt)adm = 150 MPa e a tensão de cisalhamento admissível para o pino for
adm = 85 MPa, determine o diâmetro do pino para o qual a carga P será máxima. Considere que o orifício na barra tem o mesmo diâmetro d do pino. Considere também t = 6 mm e w = 50 mm.
d = 16,29 mm
d = 19,29 mm
d = 18,29 mm
d = 17,29 mm
d = 15,29 mm
O tubo de aço A-36 tem diâmetro externo de 100 mm. Se for mantido no lugar por um cabo de ancoragem, determine, com aproximação de múltiplos de 5 mm, o diâmetro interno exigido para que ele possa suportar uma carga vertical máxima de P=20 kN sem provocar flambagem no tubo. Considere que as extremidades do tubo estão acopladas por pinos. E = 200 GPa.
dint = 95 mm
dint = 60 mm
dint = 80 mm
dint = 90 mm
dint = 45 mm
Uma coluna de aço A-36 (E= 200 GPa) tem comprimento de 4m e está presa por pinos em ambas as extremidades. Se a área da seção transversal tiver dimensões mostradas na figura, determine a carga crítica.
Pcr = 25,7 KN
Pcr = 32,7 KN
Pcr = 22,7 KN
Pcr = 27,7 KN
Pcr = 34,7 KN
A viga é construída com cinco tábuas parafusadas como mostra a figura. Determine a força de cisalhamento máxima desenvolvida em cada parafuso se o espaço entre eles for s = 250 mm e o cisalhamento aplicado for V = 35 kN.
F = 3,31 KN
F = 4,51 KN
F = 8,31 KN
F = 5,31 KN
F = 3,51 KN
Um amortecedor de vibrações é constituído por dois blocos de borracha colados à placa AB e dois suportes fixos, como mostra a figura. Determine o módulo de elasticidade transversal da borracha a ser usada, sabendo-se que, para uma força vertical P de 40 KN, o deslocamento vertical de placa AB deve ser no máximo, 3,5 mm. Considere a = 35 mm, h = 200 mm e espessura = 120 mm e E = 120 GPa.
T2 = 43,37 °C
T2 = 45,77 °C
T2 = 42,17 °C
T2 = 46,97 °C
T2 = 48,57 °C
A barra é suportada pelo pino. Se a tensão de tração admissível para a barra for (σt)adm = 150 MPa e a tensão de cisalhamento admissível para o pino for
adm = 85 MPa, determine o diâmetro do pino para o qual a carga P será máxima. Considere que o orifício na barra tem o mesmo diâmetro d do pino. Considere também t = 6 mm e w = 50 mm.
d = 16,29 mm
d = 19,29 mm
d = 18,29 mm
d = 17,29 mm
d = 15,29 mm
O tubo de aço A-36 tem diâmetro externo de 100 mm. Se for mantido no lugar por um cabo de ancoragem, determine, com aproximação de múltiplos de 5 mm, o diâmetro interno exigido para que ele possa suportar uma carga vertical máxima de P=20 kN sem provocar flambagem no tubo. Considere que as extremidades do tubo estão acopladas por pinos. E = 200 GPa.
dint = 95 mm
dint = 60 mm
dint = 80 mm
dint = 90 mm
dint = 45 mm
Uma coluna de aço A-36 (E= 200 GPa) tem comprimento de 4m e está presa por pinos em ambas as extremidades. Se a área da seção transversal tiver dimensões mostradas na figura, determine a carga crítica.
Pcr = 25,7 KN
Pcr = 32,7 KN
Pcr = 22,7 KN
Pcr = 27,7 KN
Pcr = 34,7 KN
A viga é construída com cinco tábuas parafusadas como mostra a figura. Determine a força de cisalhamento máxima desenvolvida em cada parafuso se o espaço entre eles for s = 250 mm e o cisalhamento aplicado for V = 35 kN.
F = 3,31 KN
F = 4,51 KN
F = 8,31 KN
F = 5,31 KN
F = 3,51 KN
Um amortecedor de vibrações é constituído por dois blocos de borracha colados à placa AB e dois suportes fixos, como mostra a figura. Determine o módulo de elasticidade transversal da borracha a ser usada, sabendo-se que, para uma força vertical P de 40 KN, o deslocamento vertical de placa AB deve ser no máximo, 3,5 mm. Considere a = 35 mm, h = 200 mm e espessura = 120 mm e E = 120 GPa.
adm = 85 MPa, determine o diâmetro do pino para o qual a carga P será máxima. Considere que o orifício na barra tem o mesmo diâmetro d do pino. Considere também t = 6 mm e w = 50 mm.d = 16,29 mm
d = 19,29 mm
d = 18,29 mm
d = 17,29 mm
d = 15,29 mm
O tubo de aço A-36 tem diâmetro externo de 100 mm. Se for mantido no lugar por um cabo de ancoragem, determine, com aproximação de múltiplos de 5 mm, o diâmetro interno exigido para que ele possa suportar uma carga vertical máxima de P=20 kN sem provocar flambagem no tubo. Considere que as extremidades do tubo estão acopladas por pinos. E = 200 GPa.
dint = 95 mm
dint = 60 mm
dint = 80 mm
dint = 90 mm
dint = 45 mm
Uma coluna de aço A-36 (E= 200 GPa) tem comprimento de 4m e está presa por pinos em ambas as extremidades. Se a área da seção transversal tiver dimensões mostradas na figura, determine a carga crítica.
Pcr = 25,7 KN
Pcr = 32,7 KN
Pcr = 22,7 KN
Pcr = 27,7 KN
Pcr = 34,7 KN
A viga é construída com cinco tábuas parafusadas como mostra a figura. Determine a força de cisalhamento máxima desenvolvida em cada parafuso se o espaço entre eles for s = 250 mm e o cisalhamento aplicado for V = 35 kN.
F = 3,31 KN
F = 4,51 KN
F = 8,31 KN
F = 5,31 KN
F = 3,51 KN
Um amortecedor de vibrações é constituído por dois blocos de borracha colados à placa AB e dois suportes fixos, como mostra a figura. Determine o módulo de elasticidade transversal da borracha a ser usada, sabendo-se que, para uma força vertical P de 40 KN, o deslocamento vertical de placa AB deve ser no máximo, 3,5 mm. Considere a = 35 mm, h = 200 mm e espessura = 120 mm e E = 120 GPa.
dint = 95 mm
dint = 60 mm
dint = 80 mm
dint = 90 mm
dint = 45 mm
Uma coluna de aço A-36 (E= 200 GPa) tem comprimento de 4m e está presa por pinos em ambas as extremidades. Se a área da seção transversal tiver dimensões mostradas na figura, determine a carga crítica.
Pcr = 25,7 KN
Pcr = 32,7 KN
Pcr = 22,7 KN
Pcr = 27,7 KN
Pcr = 34,7 KN
A viga é construída com cinco tábuas parafusadas como mostra a figura. Determine a força de cisalhamento máxima desenvolvida em cada parafuso se o espaço entre eles for s = 250 mm e o cisalhamento aplicado for V = 35 kN.
F = 3,31 KN
F = 4,51 KN
F = 8,31 KN
F = 5,31 KN
F = 3,51 KN
Um amortecedor de vibrações é constituído por dois blocos de borracha colados à placa AB e dois suportes fixos, como mostra a figura. Determine o módulo de elasticidade transversal da borracha a ser usada, sabendo-se que, para uma força vertical P de 40 KN, o deslocamento vertical de placa AB deve ser no máximo, 3,5 mm. Considere a = 35 mm, h = 200 mm e espessura = 120 mm e E = 120 GPa.
Pcr = 25,7 KN
Pcr = 32,7 KN
Pcr = 22,7 KN
Pcr = 27,7 KN
Pcr = 34,7 KN
A viga é construída com cinco tábuas parafusadas como mostra a figura. Determine a força de cisalhamento máxima desenvolvida em cada parafuso se o espaço entre eles for s = 250 mm e o cisalhamento aplicado for V = 35 kN.
F = 3,31 KN
F = 4,51 KN
F = 8,31 KN
F = 5,31 KN
F = 3,51 KN
Um amortecedor de vibrações é constituído por dois blocos de borracha colados à placa AB e dois suportes fixos, como mostra a figura. Determine o módulo de elasticidade transversal da borracha a ser usada, sabendo-se que, para uma força vertical P de 40 KN, o deslocamento vertical de placa AB deve ser no máximo, 3,5 mm. Considere a = 35 mm, h = 200 mm e espessura = 120 mm e E = 120 GPa.
F = 3,31 KN
F = 4,51 KN
F = 8,31 KN
F = 5,31 KN
F = 3,51 KN
Um amortecedor de vibrações é constituído por dois blocos de borracha colados à placa AB e dois suportes fixos, como mostra a figura. Determine o módulo de elasticidade transversal da borracha a ser usada, sabendo-se que, para uma força vertical P de 40 KN, o deslocamento vertical de placa AB deve ser no máximo, 3,5 mm. Considere a = 35 mm, h = 200 mm e espessura = 120 mm e E = 120 GPa.